HOME»データベーススペシャリスト平成28年春期»午前Ⅱ 問2
データベーススペシャリスト平成28年春期 午前Ⅱ 問2
問2
k次のB木構造において，ルートノードはi個(1≦i≦2k)のレコードをもち，ルート以外のノードはj個(k≦j≦2k)のレコードをもつものとする。ルートノードを1段目とした場合，B木は1段目からn段目までに最大何レコードを格納することができるか。ここで，k，nは自然数とし，n≧2とする。
- (2k＋1)n-1－1
- (2k＋1)n－1
- 2(k＋1)n-1－1
- 2(k＋1)n－1
分類
テクノロジ系 » データベース » データベース方式
正解
イ
解説
B木は、木構造内のノードの容量の尺度である次数kを基準にして、下記の特徴をもつ多分木です。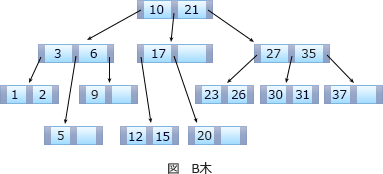
B木の各節は保持するキー数＋1個のポインタを保持します。この設問では各節は最大で2k個のレコード(キー)をもつため、各節がもつ子の個数は最大2k＋1個です。
仮にk＝2ならば、節点が保持する最大レコード数が(2×2=)4、各節点がもつ子の数が(2×2+1=)5となり、段数nが3であれば次のような木を構成します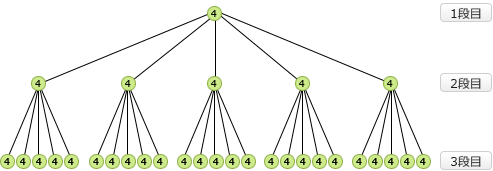
上記の木構造には節点が31個あり、レコードの総数はこれに4を乗じた124個になります。この数字をもとにすれば、選択肢の式にk=2，n=3を代入して正しく算出される「イ」が適切とわかります。
また次のように考えることも可能です。前述したk=2のケースでは段ごとのレコード数は次のように増加していきます。
したがって「イ」が正解です。
- 根は1以上2k個以下のキーをもつ
- 根以外の節はk以上2k個以下のキーをもつ
- 根から全ての葉までの深さが同じである
仮にk＝2ならば、節点が保持する最大レコード数が(2×2=)4、各節点がもつ子の数が(2×2+1=)5となり、段数nが3であれば次のような木を構成します
また次のように考えることも可能です。前述したk=2のケースでは段ごとのレコード数は次のように増加していきます。
- 1段目…4個
- 2段目…4×5＝20個
- 3段目…4×5×5＝100個
- 4段目…4×5×5×5＝500個
- n段目…4×5n-1個