分野：テクノロジ系
中分類：データベース
小分類：データベース設計

候補キー(candidate key)とは、ある関係の1つの組を一意に決定できる属性、又は属性の組合せで極小のものです。極小とはある組を一意に決定するため必要な属性以外が含まれていない様子を示します。ある関係に候補キーが1つしかない場合は自ずとそれが主キーとなり、候補キーが複数ある場合はその中から1つが主キーとして選択され、残りは代替キー(alternate key)となります。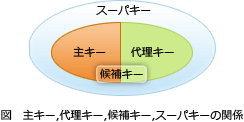設問の関数従属はX→Yという単一属性同士ではなく「X→YZ」「XY→Z」という属性と属性の和集合という関係なので、関数従属性の推論規則を適用して解きます。推論規則とはある関数従属性について必ず成立する関係のことで次に示す6つがあります。

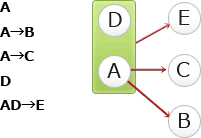
反射律

YがXの部分集合ならば、X→Y が成立する。

増加律

X→Y ならば、X∪Z→Y∪Z が成立する。

推移律

X→Y、かつ、Y→Z ならば X→Z が成立する。

擬推移律

X→Y、かつ、Y∪W→Z ならば X∪W→Z が成立する

合併律

X→Y、かつ、X→Z ならば X→Y∪Z が成立する。

分解律

X→Y∪Z ならば、X→Y、かつ、X→Zが成立する。

まず「A→BC」に分解律を適用して「A→B」「A→C」という2つの関数従属を導きます。これによってAが決定されるとA，B，C 3つの属性の値が一意に決定されることがわかります。さらに「CD→E」のCはAに関数従属しているため擬推移律の適用で「AD→E」が成立します。
AとDの組合せは、以下のように全ての属性の値が一意に決定可能、かつ、極小の組合せであるため、この組合せが関係Rの候補キーとして適切です。

• Eの値が決まらないため不適切です。
• 全ての属性の値が一意に決まりますが、Cが冗長であるため候補キーの条件を満たしません。
• 正しい。
• A，Bの値が決まらないため不適切です。