平成30年春期試験問題 午前Ⅰ 問3
正解 ウ問題へ
分野:テクノロジ系
中分類:アルゴリズムとプログラミング
小分類:データ構造
中分類:アルゴリズムとプログラミング
小分類:データ構造
広告
解説
再帰とは、実行中に自分自身を呼び出すことをいい、再帰呼出しを行っても正しい結果を返すことができる性質をもつプログラムを「再帰的プログラム」といいます。
少し長くなりますが、再帰関数の動作を理解するために例を挙げて説明します。例えば、nの階乗を再帰的に計算する関数F(n)が次のように定義されていたとします。(nは非負の整数です)
n>0のとき、F(n)=n×F(n-1)
n=0のとき、F(n)=1
階乗とは、1からある自然数nまでの相乗のことをいい、n の階乗は記号 ! を使って「n!」と表記されます。例えば 3! であれば、
3×2×1=6
というように計算します。
関数F(n)を用いて 3! を計算すると、以下のように実行途中で自分自身の呼び出しを伴います。
そして、n=0のときにF(0)が1を返し、呼出し元の処理に戻っていく過程では、最後に積み上げたものから順にF(1)、F(2)、F(3)と値が返ってきて計算されます。
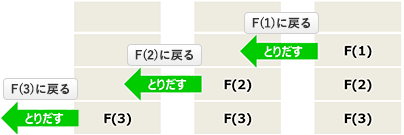 上記のように、再帰的な処理では A1→A2→A3 の順でプログラムを呼び出した場合、A3→A2→A1 というように後から入れたものから順にその値を使用します。つまり再帰的な処理は、LIFO(Last-In First-Out,後入れ先出し)の記憶管理方式を用いて実現されています。
上記のように、再帰的な処理では A1→A2→A3 の順でプログラムを呼び出した場合、A3→A2→A1 というように後から入れたものから順にその値を使用します。つまり再帰的な処理は、LIFO(Last-In First-Out,後入れ先出し)の記憶管理方式を用いて実現されています。
したがって正解は「ウ」です。
少し長くなりますが、再帰関数の動作を理解するために例を挙げて説明します。例えば、nの階乗を再帰的に計算する関数F(n)が次のように定義されていたとします。(nは非負の整数です)
n>0のとき、F(n)=n×F(n-1)
n=0のとき、F(n)=1
階乗とは、1からある自然数nまでの相乗のことをいい、n の階乗は記号 ! を使って「n!」と表記されます。例えば 3! であれば、
3×2×1=6
というように計算します。
関数F(n)を用いて 3! を計算すると、以下のように実行途中で自分自身の呼び出しを伴います。
F(3)=3×F(3-1)
//自分自身 F(2)を呼び出す
F(2)=2×F(2-1)
//F(1)を呼び出す
F(1)=1×F(1-1)
//F(0)を呼び出す
F(0)=1
//F(1)の処理に戻る
F(1)=1×1=1
//F(2)の処理に戻る
F(2)=2×1=2
//F(3)の処理に戻る
F(3)=3×2=6
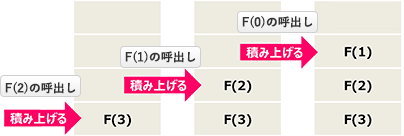
上記のように再帰的な処理では、ある関数の処理中に同じ関数(自分自身)を呼び出し、呼び出した関数の処理が終わると呼出し元の処理に戻ります。このような手順で処理されるため、最終的に正しい結果を得るためには、自分自身を呼び出した時点での呼出し元側の途中経過を記憶しておかなければなりません。再帰的な処理では、実行中に自分自身が呼び出された場合にそこまでの実行途中の状態を、スタックと呼ばれるデータ構造に格納しておきます。//自分自身 F(2)を呼び出す
F(2)=2×F(2-1)
//F(1)を呼び出す
F(1)=1×F(1-1)
//F(0)を呼び出す
F(0)=1
//F(1)の処理に戻る
F(1)=1×1=1
//F(2)の処理に戻る
F(2)=2×1=2
//F(3)の処理に戻る
F(3)=3×2=6

そして、n=0のときにF(0)が1を返し、呼出し元の処理に戻っていく過程では、最後に積み上げたものから順にF(1)、F(2)、F(3)と値が返ってきて計算されます。

したがって正解は「ウ」です。
広告