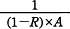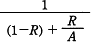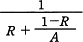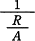平成22年春期試験問題 午前Ⅱ 問23
問23解説へ
コンピュータシステムにおいて,改善手法を適用した機能部分の全体に対する割合をR(0<R<1),その部分の改善手法を適用する前に対する適用した後の性能比をAとする。このとき,全体の性能比を表す式はどれか。
正解 イ問題へ
分野 :テクノロジ系
中分類:システム構成要素
小分類:システムの評価指標
中分類:システム構成要素
小分類:システムの評価指標
広告
解説
性能は処理時間の逆数となるので改善後の処理時間から性能を表す式を導きます。
以下、改善前の全体の処理時間を1として考えます。
まず改善を適用しない部分の割合は「1-R」で、その部分の処理時間は改善前と変わらないため、
1×(1-R)=1-R
と表せます。次に改善を適用した部分(R)の処理時間ですが、性能比(A)が2倍になれば処理時間が1/2に、3倍になれば1/3というように処理時間と性能比は逆数の関係にあるため「元の処理時間/性能比」という式で表すことができます。改善適用部分(R)の前の処理時間は「1×R」なので、改善後の処理時間は、
(1×R)/A=R/A
という式で表せます。
改善後の全体の処理時間は上記2つを足したものになるので、
(1-R)+R/A
となり、改善後の性能比はこの式の逆数である「イ」の式になります。
なおこの式は、性能向上比を表すアムダールの法則として知られています。
以下、改善前の全体の処理時間を1として考えます。
まず改善を適用しない部分の割合は「1-R」で、その部分の処理時間は改善前と変わらないため、
1×(1-R)=1-R
と表せます。次に改善を適用した部分(R)の処理時間ですが、性能比(A)が2倍になれば処理時間が1/2に、3倍になれば1/3というように処理時間と性能比は逆数の関係にあるため「元の処理時間/性能比」という式で表すことができます。改善適用部分(R)の前の処理時間は「1×R」なので、改善後の処理時間は、
(1×R)/A=R/A
という式で表せます。
改善後の全体の処理時間は上記2つを足したものになるので、
(1-R)+R/A
となり、改善後の性能比はこの式の逆数である「イ」の式になります。
なおこの式は、性能向上比を表すアムダールの法則として知られています。
広告